PROJECT

Monte-Carlo Learning

14 September, 2021

Monte-Carlo Learning
Gymnasium
Reinforcement Learning
View code

Contents

What is the Project?

Monte-Carlo (MC) Learning is an alternative method to Dynamic Programming (DP), which solves known Markov Decision Processes (MDPs). MC Learning is instead used to estimate value functions and discover optimal policies for unknown MDPs.

To understand how MC Learning works, the project focuses on the casino card game Blackjack that uses OpenAI Gym's environment and is separated into two sections: prediction and control. Prediction focuses on estimating the value functions and control discovers the optimal policies.

The Environment

Blackjack is a popular casino card game, where the user aims to obtain cards that sum as close to, or equal to, a numerical value of 21, without exceeding it. Naturally, the game is formulated as an episodic finite MDP. Full details of the rules of the environment are highlighted below:

The player plays against a fixed dealer, where:

  • Face cards (Jack, Queen, King) have the point value of 10
  • Aces can either count as 11 or 1, and is called 'usable' at 11
  • The game uses an infinite deck (with card replacements), preventing card tracking
  • The game starts with the player and dealer having one face up and one face down card

The player has two actions, hit and stick, where:

  • STICK = 0: keep the hand they currently have and move to dealers turn
  • HIT = 1: request additional cards until they decide to stop

The player busts if they exceed 21 (loses). After the player sticks, the dealer reveals their facedown card, and draws until their sum is 17 or greater. If the dealer goes bust the player wins. If neither the player nor the dealer busts, the outcome (win, lose, draw) is decided by whose sum is closest to 21.

Reward scores:

  • Win = +1
  • Draw = 0
  • Lose = -1

The observation of the environment is a tuple of 3 items:

  • The players current sum (0, 1, ..., 31)
  • The dealer's one showing card (1, ..., 10)
  • An indicator that determines the player holding a usable ace (no=0, yes=1)

The player makes decisions based on (total of 200 states):

  • Their current sum when between 12 - 21
  • The dealer's one showing card (ace - 10)
  • Whether the dealer has a usable ace

Solving the Environment

Prediction

MC Prediction provides a method for estimating value functions for unknown MDPs, enabling two methods for policy evaluation: first-visit and every-visit. Programmatic implementations are housed on GitHub. They both follow a limited policy based on the following rules:

  • Agent card sum > 18: take STICK action with 80% probability
  • Agent card sum <= 18: take HIT action with 80% probability
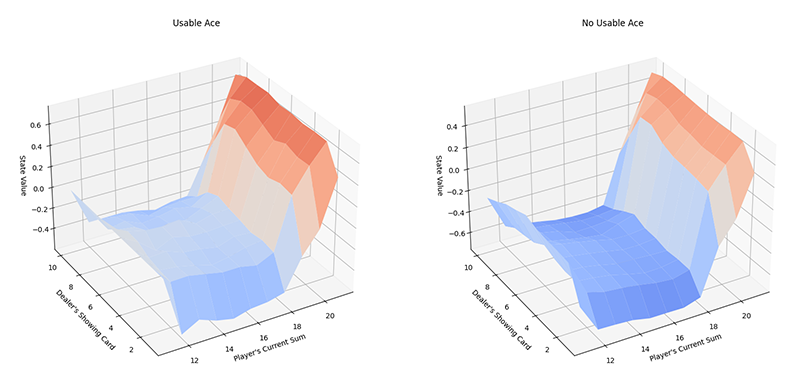
Prediction Results

Figure 1.1. Monte-Carlo Prediction results for a player with and without a usable ace.

Both methods achieved the results highlighted in figure 1.1, where the algorithms performed 500,000 episodes with a gamma of 1.0 (no discounted return). The figure shows the difference in return (state value) when the agent's sum is between 10 - 21 and the dealer's sum is between 1 - 10.

If the colour is dark-blue, the reward achieved is closer to -1 (player lose), and when it is dark-red, it is closer to +1 (player win). Whether the player has a usable ace or no usable ace, the estimated results are similar. For example, when the player's current sum is low (10 - 12), they have a higher likelihood of winning because of the greater chance of receiving cards that will get the agent closer to 21.